Find a pattern in the following
1 squared is 1; 11 squared is 121; A difference of 120
2 squared is 4; 12 squared is 144; A difference of 140
3 squared is 9; 13 squared is 169; A difference of 160
4 squared is 16; 14 squared is 196; A difference of 180
5 squared is 25; 15 squared is 225; A difference of 200
Isn't interesting(For those who have a passion for math)?
This goes on ForeverThen, for numbers ending in the number 1(1,11,21,31...)
1 squared is 1
11 squared is 121
21 squared is 441
31 squared is 961
41 squared is 1681
51 squared is 2601
61 squared is 3721
71 squared is 5041
Now obviously, the ones digit is always 1. the Tens digit goes up by 2s, and the hundreds digit goes up 1,3,5,7,0,1,3
The reason behind this is
we are figuring out:(x + 10)² - x²
Expanding out you have
x² + 20x + 100 - x²= 100 + 20x
This matches exactly with your results which is 120, 140, 160, etc.
For your second sequence.Your numbers are of the form:10x + 1
Squaring you have:(10x + 1)²= 100x² + 20x + 1
The ones digit is always 1 because of the +1.The number goes up by 20 each time because of the +20x, which means the tens digit goes up by 2.The amount above 100 goes up by a square (plus the carry from the tens digit):0, 1, 4, 9, 16, 25(+1), 36(+1), 49(+1)the difference would be odd numbers, but it bumps up by the carry on every 5 numbers.1, 3, 5, 7, 9(+1)=10-->0, 1, 3, 5, 7, 9(+1)=10-->0
Showing posts with label Some Interesting Facts. Show all posts
Showing posts with label Some Interesting Facts. Show all posts
Thursday, May 7, 2009
Monday, September 17, 2007
Catalan numbers
The Catalan Numbers express the number of ways you can divide a polygon with N sides into triangles, using non-intersecting diagonals.
Euler's formula to generate the Catalan Numbers is
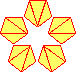
an example of catalan in a hexagon is shown in a figure.


no. of polygon sides 3 4 5 6 7 8 9
no. of ways to divide 1 2 5 14 42 132 429
Euler's formula to generate the Catalan Numbers is
2 * 6* ..... (4n-10)_____________________(n-1)!
an example of catalan in a hexagon is shown in a figure.

Hexagonal numbers

Hexagonal numbers are figurate numbers (numbers that can be represented by a regular geometric arrangement of equally spaced points), and 6-polygonal numbers of the form n(2n-1). The first few are 1, 6, 15, 28, 45, ... . Every hexagonal number is also a triangular number.
Like the triangular numbers, the hexagonal numbers are found in the third diagonal of Pascal's triangle:
Like the triangular numbers, the hexagonal numbers are found in the third diagonal of Pascal's triangle:
1 Row 0
1 1 Row 1
1 2 1 Row 2
1 3 3 1 Row 3
1 4 6 4 1 Row 4 1 5 10 10 5 1 Row 5
1 6 15 20 15 6 1 Row 6
1 7 21 35 35 21 7 1 Row 7
1 8 28 56 70 56 28 8 1 Row 8
Triangular numbers
A triangular number is a figurate number: a number that can be represented by a regular geometric arrangement of equally spaced points. Triangular numbers can be thought of as the numbers of dots you need to make a triangle:
The numbers in red colour are triangular numbers.
The triangular numbers are found in the third diagonal of Pascal's triangle:
1 Row 0
1 1 Row 1
1 2 1 Row 2
1 3 3 1 Row 3
1 4 6 4 1 Row 4
1 5 10 10 5 1 Row 5
1 6 15 20 15 6 1 Row 6
1 7 21 35 35 21 7 1 Row 71 8 28 56 70 56 28 8 1 Row 8
The numbers in red colour are triangular numbers.
Sierpinski Triangle
The Sierpinski Triangle is a famous fractal that forms a geometric pattern as the midpoints of the sides of a triangle are connected, creating four more triangles the sides of which are then connected, and so on.

If you color the odd numbers in Pascal's triangle and shade out all the other spaces, you will see Sierpinski's triangle.

--------------------------------------------------------------------------------

If you color the odd numbers in Pascal's triangle and shade out all the other spaces, you will see Sierpinski's triangle.

--------------------------------------------------------------------------------
Wednesday, September 12, 2007
Amicable numbers
Amicable Numbers
Amicable numbers are two numbers so related that the sum of the proper divisors of the one is equal to the other, one being considered as a proper divisor but not the number itself.
e.g Proper divisors of 220 are 1, 2, 4, 5, 10, 11, 20, 22, 44, 55 and 110
proper divisors of 284 are 1,2,4,71 and 142
1 + 2 + 4 + 5 + 10 + 11 +20 + 22 + 44 + 55 + 110 = 284
1 + 2 + 4 + 71 + 142 = 220
thus 220 and 284 are amicable numbers.
Numbers 2620 and 2924 are pair of amicable numbers as proper factors of 2620 are 1, 2, 4, 5, 10, 20, 131, 262, 524, 655, 1310 and proper factors of 2924 are 1, 2, 4, 17, 34, 43, 68, 86, 172, 731,1462
1+ 2+ 4+ 5+ 10+ 20+ 131+ 262+ 524+ 655+ 1310 = 2924
1+ 2+ 4+ 17+ 34+ 43+ 68+ 86+ 172+ 731+ 462 = 2620.
try out for more such numbers.
Amicable numbers are two numbers so related that the sum of the proper divisors of the one is equal to the other, one being considered as a proper divisor but not the number itself.
e.g Proper divisors of 220 are 1, 2, 4, 5, 10, 11, 20, 22, 44, 55 and 110
proper divisors of 284 are 1,2,4,71 and 142
1 + 2 + 4 + 5 + 10 + 11 +20 + 22 + 44 + 55 + 110 = 284
1 + 2 + 4 + 71 + 142 = 220
thus 220 and 284 are amicable numbers.
Numbers 2620 and 2924 are pair of amicable numbers as proper factors of 2620 are 1, 2, 4, 5, 10, 20, 131, 262, 524, 655, 1310 and proper factors of 2924 are 1, 2, 4, 17, 34, 43, 68, 86, 172, 731,1462
1+ 2+ 4+ 5+ 10+ 20+ 131+ 262+ 524+ 655+ 1310 = 2924
1+ 2+ 4+ 17+ 34+ 43+ 68+ 86+ 172+ 731+ 462 = 2620.
try out for more such numbers.
Subscribe to:
Posts (Atom)

